SVM 模型
SVM 是一种二分类模型。假设训练集中的样本是线性可分的, SVM 的目的是找到一个分类超平面,使得间隔最大化。满足间隔最大化的解是唯一的。
根据模型的复杂程度,SVM可分为线性可分支持向量机、线性支持向量机和非线性支持向量机。
函数间隔和几何间隔
对数据进行预测,该点离分类超平面越远说明本次预测的置信度越高,反之说明置信度低。在分类超平面确定时,可以通过 $ | \omega \cdot x + b | $ 反映点 $ x $ 和分类超平面的距离,由于符号表明本次预测的分类结果,所以可以用 $ y ( \omega \cdot x + b ) $ 同时对正确性和置信度进行描述。
称:
\[\hat{\gamma}_i = y_i ( \omega \cdot x_i + b )\]为超平面关于样本点的函数间隔,同时定义超平面关于数据集的函数间隔 $ \hat{\gamma} $ 为所有样本点的函数间隔的最小值。
但使用函数间隔来选择超平面还不够完善,只需要给 $ \omega $ 和 $ b $ 同时乘一个系数,就可以使分类超平面不变的情况下,使函数间隔就任意大。
可以添加一些约束条件使得间隔确定。称:
\[\gamma_i = y_i ( \frac{\omega}{||\omega||} \cdot x_i + \frac{b}{||\omega||} )\]为超平面关于样本点的几何间隔,同时定义超平面关于数据集的几何间隔 $ \gamma $ 为所有样本点的几何间隔的最小值。
从以上两式可以得知函数间隔和几何间隔之间的关系:
\[\gamma = \frac{\hat{\gamma}}{||\omega||}\]当 $ ||\omega|| = 1 $ 时,函数间隔和几何间隔一致。
线性可分 SVM 模型
模型
给定线性可分的训练集,通过间隔最大化找出来的分类超平面为:
\[\omega^{*}\cdot x +b^{*} = 0\]分类决策函数为:
\[f(x) = sign(\omega^{*}\cdot x +b^{*})\]该模型称为线性可分支持向量机。
间隔最大化的方法
首先描述以下这个问题:
\[\begin{align} \max_{\omega, b}\ & \gamma \\ s.t.\ & y_i ( \frac{\omega}{||\omega||} \cdot x_i + \frac{b}{||\omega||} )\ge \gamma , i = 1, 2, ..., N \end{align}\]根据函数间隔和几何间隔之间的关系,改写为:
\[\begin{align} \max_{\omega, b}\ & \frac{\hat{\gamma}}{||\omega||} \\ s.t.\ & y_i ( \omega \cdot x_i + b )\ge \hat{\gamma} , i = 1, 2, ..., N \end{align}\]由于函数间隔可以在不改变超平面的情况下任意缩放,所以令 $ \hat{\gamma} = 1 $,得到:
\[\begin{align} \max_{\omega, b}\ & \frac{1}{||\omega||} \\ s.t.\ & y_i ( \omega \cdot x_i + b ) - 1 \ge 0 , i = 1, 2, ..., N \end{align}\]考虑到凸函数更好进行优化,最大化 $ \frac{1}{||\omega||} $ 和最小化 $ \frac{1}{2}||\omega||^2 $ 问题可以看作等价的,得到:
\[\begin{align} \min_{\omega, b}\ & \frac{1}{2}||\omega||^2 \\ s.t.\ & y_i ( \omega \cdot x_i + b )\ge \hat{\gamma} , i = 1, 2, ..., N \end{align}\]构成了一个凸二次规划问题。
构建 Lagrange 函数,并对其对偶问题进行求解就可以得到本问题中线性可分支持向量机的参数。
支持向量
在线性可分的情况下,距离超平面最近的样本称为支持向量,根据上一节谈到的约束条件,在超平面:
\[\omega \cdot x + b = 1\]的正例和在超平面
\[\omega \cdot x + b = -1\]的负例构成支持向量,这两个超平面的距离为 $ \frac{2}{||\omega||} $。
在决定分离超平面时,只有支持向量起作用,其它实例点不起作用。
$ $
线性 SVM
模型
由于实际数据中存在误差和噪声,同时考虑到不同数据服从的分布不同,所以实际数据几乎没有线性可分的。在线性不可分的情况下上文中所讲的:
\[\begin{align} \min_{\omega, b}\ & \frac{1}{2}||\omega||^2 \\ s.t.\ & y_i ( \omega \cdot x_i + b )\ge 1 , i = 1, 2, ..., N \end{align}\]中的约束项就不满足,优化问题就进行不下去了。
考虑到这个问题,我们可以对数据集引入松弛变量 $ \xi_i \ge 0 $ 使约束条件变为:
\[y_i ( \omega \cdot x_i + b )\ge 1 - \xi_i , i = 1, 2, ..., N\]然后,令目标问题为:
\[\frac{1}{2}||\omega||^2 + C\sum_{i=1}^{N}\xi_i\]式中, $ C \gt 0 $ 为惩罚参数。这样对误分类的要求降低,同时可以通过控制惩罚参数来经可能降低误分类点。
整个优化问题可以写为:
\[\begin{align} \min_{\omega, b}\ & \frac{1}{2}||\omega||^2 + C\sum_{i=1}^{N}\xi_i \\ s.t.\ & y_i ( \omega \cdot x_i + b )\ge 1 - \xi_i , i = 1, 2, ..., N \\ & \xi_i \ge 0, i = 1, 2, \dots, N \end{align}\]这样就可以针对不严格线性可分的数据集进行训练了。
$ $
非线性支持向量机
非线性分类问题是指采用非线性模型才能进行分类的问题,如下图所示
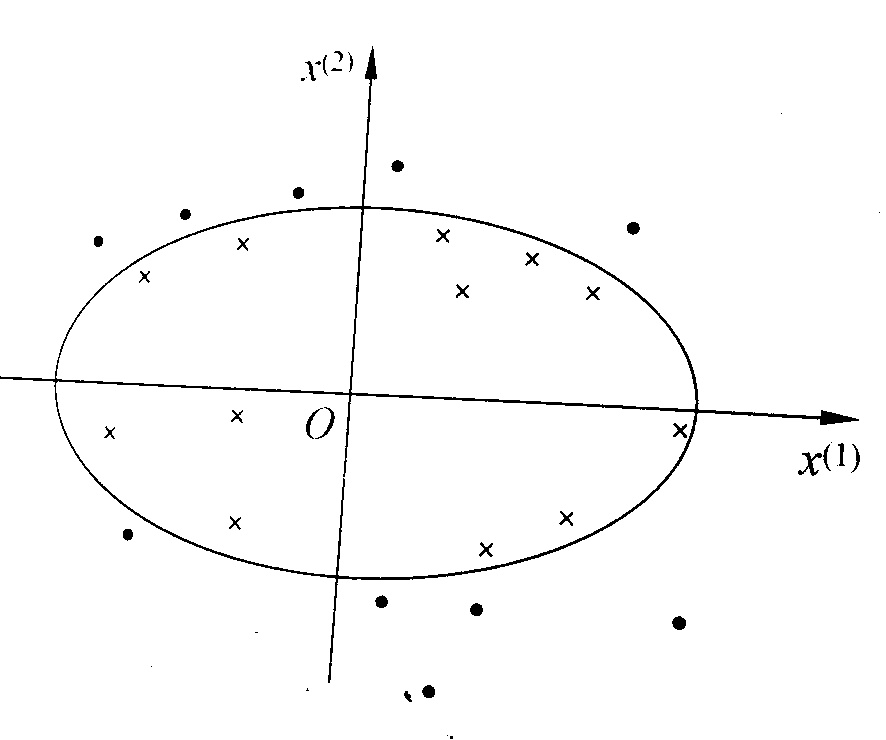
采用类似于椭圆的分类器才能对数据进行分类。此时需要采用某些方法,将原始数据从非线性空间映射到线性空间,然后在采用线性的分类方法,就能进行较好的分类。
例如设原始数据 $ x = ( x^{(1)}, x^{(2)} )^T $,新空间 $ z = (z^{(1)}, z^{(2)} )^T $,定义映射:
\[z = \phi(x) = ((x^{(1)})^2, (x^{(2)})^2)^T\]那么,原始空间中的分类平面
\[\omega_1 (x^{(1)})^2 + \omega_2 (x^{(2)})^2 + b = 0\]就会映射到
\[\omega_1 z^{(1)} + \omega_2 z^{(2)} + b = 0\]这样就可以用线性分类问题的思路解决了。
核方法
如果存在一个从 $ X \rightarrow H $ 的映射:
\[\phi(x): X \rightarrow H\]使得所有 $ x,z \in X $ ,函数
\[K(x,z) = \phi(x)\cdot\phi(z)\]则称 $ K(x,z) $ 为核函数,$ \phi(x) $ 为映射函数。式中 $ \phi(x)\cdot\phi(z) $ 为 $ \phi(x) $ 和 $ \phi(z) $ 的内积。
优化问题求解中的目标函数包含训练集中样本的俩俩内积,同时决策函数中也包括了输入样本和训练集中样本的内积,我们可以将这些问题中的内积替换为核函数,就可以将非线性问题映射到另一个空间中,作为线性问题求解。
$ $
一些对我来说不显然的地方
高中的立体几何忘得差不多了 :-(
1. $ \omega \cdot x + b = 0 $ 为什么是平面
已知平面 $ P $ ,设其法向量为 $ \omega $,设 $ Q $ 为平面内一定点,$ A $ 为平面内任意一点,有:
\[\begin{align} \vec{AQ}\perp\vec{\omega} \Rightarrow& \vec{AQ} \cdot \vec{\omega} = 0 \\ \Rightarrow& (\vec{OQ} - \vec{OA}) \cdot \vec{\omega} = 0 \\ \Rightarrow& \vec{OQ} \cdot \vec{\omega} - \vec{OA} \cdot \vec{\omega} = 0 \end{align}\]令 $ x = \vec{OQ}, b = -\vec{OA} \cdot \vec{\omega}$ 则有:
\[\omega \cdot x + b = 0\]显然,对于所有的 $ x \in P $ ,均有 $ \omega \cdot x + b = 0 $ ;若 $ x \not\in P $ ,则必然 $ \omega \cdot x + b \neq 0 $ 。
故 $ \omega \cdot x + b = 0 $ 表示一个平面。
2. $ | \omega \cdot x + b | $ 为什么反映了平面外一点到平面的距离
已知平面 $ P $ ,设其法向量为 $ \omega $,设 $ Q $ 为平面内 $ \omega $ 的起点,$ A $ 为平面外一点,如下图所示,
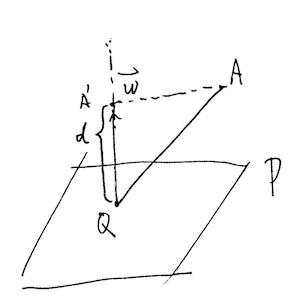
显然,$ A $ 点在 $ \omega $ 方向上的投影 $ A’ $ 到 $ Q $ 点之间的距离 $ d $ 为 $ A $ 点到平面 $ P $ 的距离。
设 $ \vec{QA} $ 和 $ \omega $ 的夹角为 $ \theta $ ,则有:
\[\begin{align} d =& |\vec{QA}| \cos \theta \\ =& |\vec{QA}| \frac{ \vec{QA} \cdot \vec{\omega} }{|\vec{QA}|\times|\vec{\omega}|} \\ =& \frac{ \vec{QA} \cdot \vec{\omega} }{|\vec{\omega}|} \\ =& \frac{1}{|\vec{\omega}|}(\vec{\omega}\cdot\vec{OA}-\vec{\omega}\cdot\vec{OQ}) \\ 由于Q \in P,所以\vec{OQ} \cdot \vec{\omega} + b = 0,故:\\ =& \frac{1}{|\vec{\omega}|}(\vec{\omega}\cdot\vec{OA}+b) \\ \end{align}\]故$ | \omega \cdot x + b | $ 为什么反映了平面外一点到平面的距离。
$ $
Initial push @ 2020-09-28
Update 1 @ 2020-10-07
Update 2 @ 2020-10-12