模型
决策树是一种基础的分类和回归方法,这里仅对其分类作用进行讨论。决策树模型呈现树状结构,基于特征对实例进行分类,它可以认为是 if-then 规则的集合。下图是利用 Sklearn 实现的决策树对 MNIST 数据集进行分类的可视化结果,可以很容易的从中看出 if-then 结构。
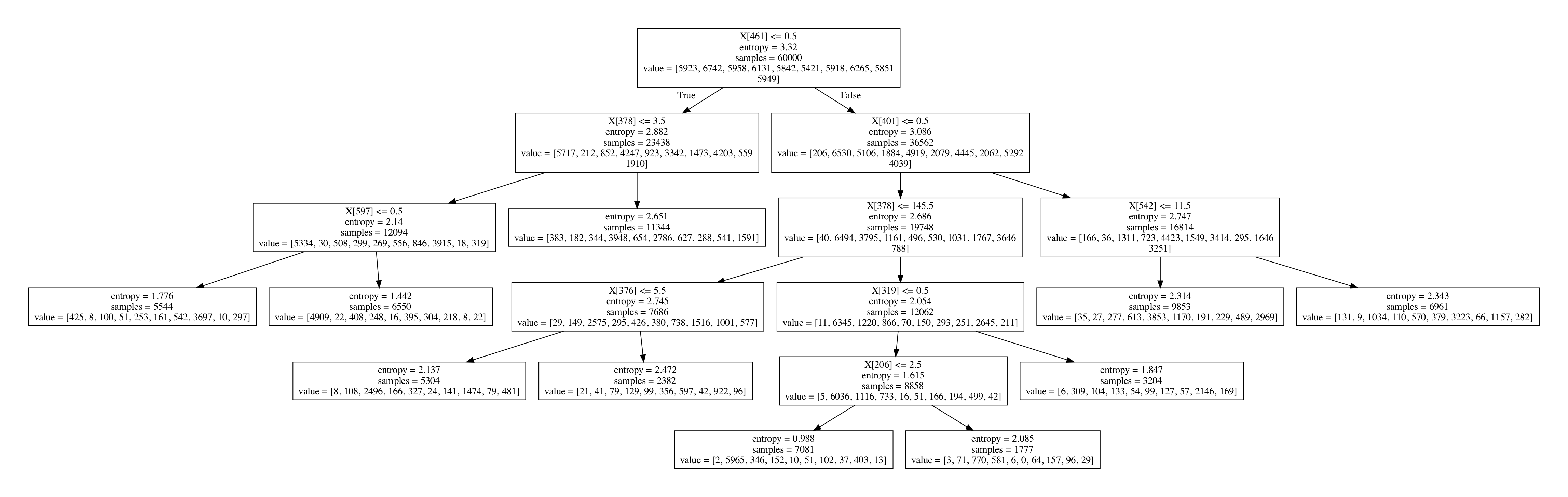
决策树由节点和有向边组成,节点分为内部节点(表示一个特征或属性)和外部节点(表示一个类)。
给定训练集
\[D = \lbrace (x_1, y_1), ..., (x_N, y_N)\rbrace\]其中 $ x_i $ 为输入的特征向量, $ y_i $ 为类标签, $ N $ 为样本容量。决策树学习的目标就是根据训练集构建一个决策树模型,使其可以对实例进行正确的分类。
特征选择
特征选择的目的是从训练集中选择具有分类能力的特征,用来划分特征空间。
熵与信息增益
熵是随机变量不确定性的度量,定义为:
\[H(X) = -\sum_{i=1}^{n} p_i \log p_i\]其中 $ p_i = P(X=x_i), i = 1, …, n $,熵越大,随机变量的不确定性越大。
定义条件熵为:
\[H(Y|X) = \sum_{i=1}^{n} p_i H(Y|X=x_i)\]则可以定义信息增益 $ g $ 为:
\[g(D, A) = H(D) - H(D|A)\]信息增益反映了在了解特征 $ A $ 的信息后,使得类 $ Y $ 信息的不确定性减少的程度。在进行特征选择时,选择信息增益较大的特征作为分类条件会使其具有更强的分类能力。
由于信息增益会倾向于选择取值较多的特征,所以可以采用信息增益比来对此问题进行矫正。
信息增益比定义为:
\[g_R(D, A) = \frac{g(D, A)}{H_A(D)} = \frac{g(D, A)}{-\sum_{i=1}^{n}\frac{|D_i|}{D} \log \frac{|D_i|}{D}}\]剪枝
决策树的生成算法会递归产生决策树,直到不能继续下去。这种算法倾向与构建复杂的决策树,使训练集的分类很准确,但会降低模型的泛化能力。对于这一问题的解决方法是考虑决策树的复杂度,对已生成的决策树进行简化。
这种简化的过程称为剪枝,其具体过程是通过某种方法,从已经生成的决策树上裁掉一些子树或叶子结点,使其父节点作为新的叶子结点。
可以定义决策树的损失函数,并通过最小化损失函数来实现剪枝。
首先定义经验熵:
\[H_t = -\sum_k \frac{N_{tk}}{N_t}\log \frac{N_{tk}}{N_t}\]定义模型对训练数据的预测误差:
\[C(T) = \sum_{t=1}^{|T|}N_tH_t(T) = -\sum_{t=1}^{|T|}\sum_{k=1}^{K}N_{tk}\log \frac{N_{tk}}{N_t}\]最后,定义损失函数为:
\[C_{\alpha}(T) = C(T) +\alpha |T|\]其中,树 $ T $ 的叶子节点数量为 $ |T| $ , $ t $ 是 $ T $ 的叶子节点,该节点由 $ N_t $ 个样本点,其中 $ k $ 类样本点由 $ N_{tk} $ 个, $ \alpha \le 0 $ 为参数。